This is a mathematical post which is related to the xkcd 936 comic about password strength. The central question is: What is better for passwords? A password containing a few random characters or a passphrase containing a (less) few random words? Here comes a mathematical discussion.
At first, here is the comic (if you do not already know it…):
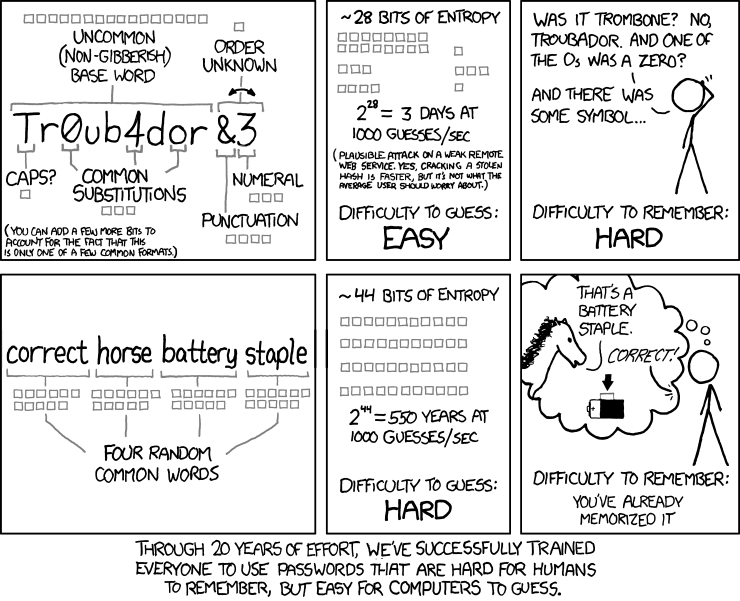
The xkcd comic concludes that is it better to use a passphrase of 4 random words rather than a single-word password which has some known substitutions in it. It further presents some statistics about the entropy of the passwords. I wanted to prove this password strength and wanted to calculate the differences between a few password settings. (I say “password” when referring to a random password chosen from characters while I state “passphrase” when referring to a password made of words.)
How to Break Passwords
I assume that each character (or word) of the password is chosen completely random! That is: The passwords/passphrases used in this scenario are generated from a truly random source and not from a human. (E.g., use the password generator in KeePass to generate random passwords, explained here.) The only chance to break these passwords is via brute-force. That is: A machine must try every single possible combination of characters in the case of the password. For cracking the passphrase, a brute-force attack in conjunction with a dictionary attack is used. That is: Every combination of words is tested against the passphrase. (In any case: I assume that the attacker actually has the possibility to test the brute-force generated passwords against the real password, e.g., in comparing the hash-values as he might know the hash from the real password, or the like.)
The Math Behind
Well, it’s only a bit of math to calculate the strength of a password. This is basically the entropy of the password since it is chosen completely random. To calculate the entropy of a password, the character set is raised to the power of the password length: . For example, when using 83 different characters for a password with only 4 chars, the calculation would be
. That is, we would have 47458321 different possibilities for the password resulting in 26 bits of entropy. (The bits of entropy are calculated with
. If a calculator has only the
or
functions, the following algorithm can be used:
.)
I used a character set for the password of 83 different characters (a-z, A-Z, 0-9, as well as the following symbols: !"$%&/()=<>+*#',;.:-_). For the generation of the passphrase I assume that the language has about 200,000 words. This might be true for the German language while the English language might have about 500,000 words (reference1 reference2). However, since the owner of the passphrase should be able to write it correctly, the vocabulary from which the passphrase is chosen should not be too complicated. ;) That is, I think 200,000 words is a good point to start. Anyway, I also calculated the values for a passphrase chosen out of 10,000 words if a really easy set of known words is used.
A “good/strength” password should have about 80 bits of security, i.e., different possibilities for the random passwords. That is, a brute-force attack would need to test
different passwords to do an exhaustive key search. (Yes, I know, one could assume that such a machine only needs
tries to find the password since it locates the correct one approximately after the half key space. However, this 1 bit does not make the difference here.)
Calculated Values
I have calculated the entropy values for the following charsets: 10 digits, 83 chars, 94 chars, 10k words, 200k words, and 500k words. Then I calculated the entropy in bits while I rounded down the bit values. So, here comes the main graph: The x-axis shows the number of characters (password) respectively the number of words (passphrase) for the random chosen passwords/passphrases, while the y-axis shows the bits of entropy which the password/passphrase actually has. (The raw values for the calculations can be found at the end of this post.)
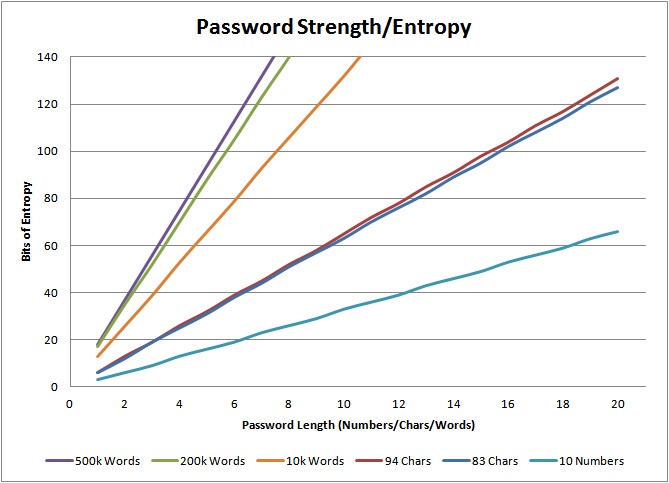
–> That is: To have 80 bits of security, a password needs about 13 characters while a passphrase only needs about 5 words! However, a passphrase chosen out of 10,000 words needs 7 words to have the same strength. <–
Since most passwords today have only 8 chars (51 bits of entropy), a passphrase with only 3 words (52 bits of entropy) would fit!
Some Interpretations
When moving from the bottom to the top of the lines in the graph we see that passwords chosen out of the 10 digits are not that secure. For example, a password with a length of 4 digits only has an entropy of 13 bits, and even 12 digits only have an entropy of 39 bits. So: don’t ever use only digits for critical passwords!
An interesting fact is the very small difference between passwords that are chosen out of 83 chars compared to passwords chosen out of 94 chars (blue and red line). I always thought that it is much more secure to use almost all possible characters for the generation of passwords, although I knew that the end-users won’t be happy if I allocate such passwords to them. But we can see that the entropy does not increase that much when adding all strange characters to the passwords. For example: A password with 8 characters has an entropy of 51 bits when chosen out of 83 chars, while it has 52 bits (only 1 more!) when chosen out of 94 chars. But if we extend the password to a length of 10, the 83 charset achieves an entropy of 63 bits, which is 12 bits more than before! However, to have at least 80 bits of entropy, you should use not less than 13 characters for your passwords.
It is easy to see that the complexity of the passphrases increases much faster than those from passwords. In fact, a 4-word passphrase chosen out of 200,000 words has an entropy of 70 bits. Now here comes the same effect as mentioned in the paragraph before: Increasing the set of words from 200k to 500k (e.g., using two languages) does not increase the security that much: only from 70 to 75 bits in the case of 4 words. But: Going from 4 to 5 words in the set of 200k words increases the entropy from 70 to 88 bits! That is: Use your mother tongue and a length of 5 words and you are secure! ;)
Concerning the passphrases chosen out of 10,000 words: This requires to have at least 7 words to gain an entropy greater than 80 bits. Ok, this is possible to remember, but I think it is getting a bit annoying if you have to remember such huge sentences for your passphrases. So: Don’t use such small dictionaries for your passphrase generation.
Increasing the Complexity
What about ideas like “I am additionally using some characters between my randomly chosen words to increase the complexity”? Well, let’s make an example: If you have 4 random words in your passphrase already and add 2 chars out of the 83 charset in random positions between the words, this would give you 20 different positions while each position would have possibilities, resulting in
more possible passphrases for each passphrase. The number of passphrases would be
which results in an entropy of 87 bits. This actually is a much higher entropy than the 70 bits of entropy from the 4 word passphrase!
(Do not confuse this idea with the method of adding the 83 charset to your 200k words for choosing the passphrase with only 4 words. It really does not matter whether you are using 200,000 or 200,083 “words” for your passphrases.)
Problems With Passphrases
To say it one more time: Your passphrases need to be randomly generated! (As well as your passwords, of course.) Do not generate your own “good” passphrase by just looking around in the room you are sitting in and concatenating the things you see to generate a passphrase.
The same behaves if you choose your passphrases out of some random suggestions. That is: If the passphrase generator you are using shows some examples of the just generated passphrases, you should NOT choose the one which looks very easy to you. The reason is, that when you choose a passphrase manually, it decreases the entropy since an attacker will always start its brute-force attacks with the simplest word sets. This is really important. You should not generate your passphrases yourself nor should you choose “easy” passphrases out of randomly generated ones!
Another general problem when using long passphrases is the input length of password fields in the applications/services you are using. I have had many services that limit the input for passwords to 16 (or the like) characters. But a passphrase with at least 4 words will have more than 16 chars. Hm, bad news… (Hopefully the application tells you that your password is too long and does not simply cut it after the maximum input size ;))
Conclusion
Coming back to the xkcd comic: Yes, it is more secure to use a passphrase with 4 words than a password. And yes, it would be much easier for humans to remember such a passphrase. However, the complexity bits shown in the comic are not based on the mathematic I have shown in this post, but are suggestions from not randomly generated passwords.
If chosen completely random, a passphrase with 4 words has the same complexity as a password with 11 characters. Since it is more applicable for an end-user to use a passphrase, this method should be preferred. And it should be much easier for the security engineer to motivate the users to learn a passphrase than a random password. ;)
However, if you are using more than 10 different applications and want to allocate 10 different passwords/passphrases, you are lost anyway! So my advice is still to use a password safe such as KeePass with a really strength password/passphrase as the master password! (A german KeePass introduction can be found here on my blog.)
Appendix: Raw Values
The following tables show the raw values used for the figure above. The first one lists the length of the passwords (count of characters for passwords respectively the count of words for passphrases) and the number of different passwords for each character set. The second one shows the corresponding security complexities = password entropies.
| Length | 10 Numbers | 83 Chars | 94 Chars | 10k Words | 200k Words | 500k Words |
|---|---|---|---|---|---|---|
| 1 | 10 | 83 | 94 | 10000 | 200000 | 500000 |
| 2 | 100 | 6889 | 8836 | 100000000 | 40000000000 | 2,5E+11 |
| 3 | 1000 | 571787 | 830584 | 1E+12 | 8E+15 | 1,25E+17 |
| 4 | 10000 | 47458321 | 78074896 | 1E+16 | 1,6E+21 | 6,25E+22 |
| 5 | 100000 | 3939040643 | 7339040224 | 1E+20 | 3,2E+26 | 3,125E+28 |
| 6 | 1000000 | 3,2694E+11 | 6,8987E+11 | 1E+24 | 6,4E+31 | 1,5625E+34 |
| 7 | 10000000 | 2,71361E+13 | 6,48478E+13 | 1E+28 | 1,28E+37 | 7,8125E+39 |
| 8 | 100000000 | 2,25229E+15 | 6,09569E+15 | 1E+32 | 2,56E+42 | 3,90625E+45 |
| 9 | 1000000000 | 1,8694E+17 | 5,72995E+17 | 1E+36 | 5,12E+47 | 1,95313E+51 |
| 10 | 10000000000 | 1,5516E+19 | 5,38615E+19 | 1E+40 | 1,024E+53 | 9,76563E+56 |
| 11 | 1E+11 | 1,28783E+21 | 5,06298E+21 | 1E+44 | 2,048E+58 | 4,88281E+62 |
| 12 | 1E+12 | 1,0689E+23 | 4,7592E+23 | 1E+48 | 4,096E+63 | 2,44141E+68 |
| 13 | 1E+13 | 8,87187E+24 | 4,47365E+25 | 1E+52 | 8,192E+68 | 1,2207E+74 |
| 14 | 1E+14 | 7,36365E+26 | 4,20523E+27 | 1E+56 | 1,6384E+74 | 6,10352E+79 |
| 15 | 1E+15 | 6,11183E+28 | 3,95292E+29 | 1E+60 | 3,2768E+79 | 3,05176E+85 |
| 16 | 1E+16 | 5,07282E+30 | 3,71574E+31 | 1E+64 | 6,5536E+84 | 1,52588E+91 |
| 17 | 1E+17 | 4,21044E+32 | 3,4928E+33 | 1E+68 | 1,31072E+90 | 7,62939E+96 |
| 18 | 1E+18 | 3,49467E+34 | 3,28323E+35 | 1E+72 | 2,62144E+95 | 3,8147E+102 |
| 19 | 1E+19 | 2,90057E+36 | 3,08624E+37 | 1E+76 | 5,2429E+100 | 1,9073E+108 |
| 20 | 1E+20 | 2,40748E+38 | 2,90106E+39 | 1E+80 | 1,0486E+106 | 9,5367E+113 |
| Length | Entropy 10 Numbers | Entropy 83 Chars | Entropy 94 Chars | Entropy 10k Words | Entropy 200k Words | Entropy 500k Words |
|---|---|---|---|---|---|---|
| 1 | 3 | 6 | 6 | 13 | 17 | 18 |
| 2 | 6 | 12 | 13 | 26 | 35 | 37 |
| 3 | 9 | 19 | 19 | 39 | 52 | 56 |
| 4 | 13 | 25 | 26 | 53 | 70 | 75 |
| 5 | 16 | 31 | 32 | 66 | 88 | 94 |
| 6 | 19 | 38 | 39 | 79 | 105 | 113 |
| 7 | 23 | 44 | 45 | 93 | 123 | 132 |
| 8 | 26 | 51 | 52 | 106 | 140 | 151 |
| 9 | 29 | 57 | 58 | 119 | 158 | 170 |
| 10 | 33 | 63 | 65 | 132 | 176 | 189 |
| 11 | 36 | 70 | 72 | 146 | 193 | 208 |
| 12 | 39 | 76 | 78 | 159 | 211 | 227 |
| 13 | 43 | 82 | 85 | 172 | 228 | 246 |
| 14 | 46 | 89 | 91 | 186 | 246 | 265 |
| 15 | 49 | 95 | 98 | 199 | 264 | 283 |
| 16 | 53 | 102 | 104 | 212 | 281 | 302 |
| 17 | 56 | 108 | 111 | 225 | 299 | 321 |
| 18 | 59 | 114 | 117 | 239 | 316 | 340 |
| 19 | 63 | 121 | 124 | 252 | 334 | 359 |
| 20 | 66 | 127 | 131 | 265 | 352 | 378 |
Other References
If you are interested in other discussions about password security, refer to the following pages:
- Passphrase Complexity Guidelines from the University of California, Berkeley
- Considerations from the creator of the xkcd comic
- explain xkcd – 936: Password Strength
- Checking Password Complexity with John the Ripper
Featured image: “altonaer waagenbau” by Martin Schmid is licensed under CC BY-ND 2.0.



“…….If you have 4 random words in your passphrase already and add 2 chars out of the 83 charset in random positions between the words, this would give you 20 different positions……”
Could you explain that is some more detail? I see just 5 positions to insert 2 random characters like A1… A5. In practice only 4 since the position of A1 will probably not be used.
A1 word1 A2 word2 A3 word3 A4 word4 A5
(spaces inserted just for readability)
And if you’d allow splitting the 2 characters, I see just 10=4+3+2+1 positions
A word1 1 word2 word3 word4
A word1 word2 2 word3 word4
A word1 word2 word3 3 word4
A word1 word2 word3 word4 4
word1 A word2 5 word3 word4
etc.
Hi. My idea was to add 2 independent chars, lets say x and y. Then you could have something like this (say, the 4 words are 1 2 3 4):
xy1234
x1y234
x12y34
x123y4
x1234y
1xy234
1x2y34
1x23y4
1x234y
12xy34
12x3y4
12x34y
123xy4
123x4y
1234xy
= 15 options.
I further thought of the 5 options in which only 1 char is inserted (which gives a total of 20 different options):
x1234
1×234
12×34
123×4
1234x
But here you are right: My calculation about the 83 * 83 is a bit wrong, since this is only true for the 15 options with both chars, and not for the 5 with only one char. Hm. So it must be a bit more precise for the calculation, though it should not be that much away from mine. Something like this:
200000^4 * 15 * 83 * 83 + 200000^3 * 5 * 83
Thanks for the hint. It took my some time to rebuilt my thoughts. ;)
Please check all my other calculations, too, and tell me, if there are more mistakes!
Thanks for the details, Sorry I did not add up my 5 and 10 cases, which I should have. I agree that the original estimate is a good one.
Diceware suggests a related strengthening scheme: Add just 1 random character/symbol at a random place in a generated phrase, and some 10 bits of entropy will be gained.
FYI, I have successfully used you raw value table as a reference to check numbers generated by my passphrase generator and tester SimThrow. I checked it up to 8 words of the 10K, 200K and 500K dictionaries.
Much appreciated – And first time i’ve seen secure share buttons =)
Let’s say you mix cases in your dictionary words. That would make a huge difference, would it not? To find a 5-character word in the dictionary, the hacker would have to make 52*52*52*52*52 passes through the dictionary. So easy-to-remember rules like capitalizing all vowels, or the second letter of every word, etc., would appear to make dictionaries too large to be useful.
Yes, correct. It would increase the security if you have further rules such as capitalizing several letters. BUT ONLY if you are doing it randomly! If you always capitalize the vowels, (and if the hackers knows that), you have NOT increased anything!
However, it is not necessary at all if you are already using 5 words, since the bits-of-security are already enough. ;)
I usually try to tailor the password security to the function. On a limited access computer where the only remote access is with ssh using RSA and DSA keys, the passwords may be short and relatively simple.
On the other hand, for computers accessible over the internet, I frequently use nonsense phrases of varying lengths up to just less than 100 characters.
I’ve also used directions from one place to another as a passphrase. For example “Jack’s Laundry Washington North 15th Main Ralph’s Bank”. While not random, the choice of source and destination is pretty much random from a limited set of selections but with non official names (from where Jack does his laundry to where Ralph works as a teller) and the directions may not be the most direct or the most obvious. Alternatively, it could just be a couple of places with their address “Smith’s Church 101 North Vermont Sally’s Neighbor 503 Elm”.
And then there are the formula along with a couple of extra words such as “E^2 = m^2 + p^2 gravitational hedgehog”.
One thing that I’ve found is to never use two passphrases that begin with the same word. I did that once and was always confusing the two passphrases.
Based on xkcd and the blog post above, I hacked a little tool which generates a passphrase accordingly. Just to get an impression on how it might feel to use passphrases instead passwords. The words are randomly taken from a plain-text dictionary (in my case de-en).
On my first attempts I failed to memorize the proposed passphrases. The trick, like it was also mentioned in the xkcd, is to think out a causal relation between the words. But with ‘truly’ random words, that is hard to achieve. Plus, more words than expected that are coming up are unfamiliar to me which increases that problem.
On the other hand, from my experience I do memorize 12 to 16 character passwords in the 94 Chars class, just by training the pattern on how to type that password on my keyboard. Of course, keyboard layout changes are a big hurdle.
Well, the bottom line is, in either case you have to take your time to train and memorize your secret continuously. That is why I do not use keyrings or keyagents [exceptions have a short lifetime for passwords] in order to keep my brain trained to type my passwords over and over again.
Cheers,
Don’t know how they get 28 bits of entropy with the first example, this way this is calculated is for me totally wrong.
You have case senstive alphanum + symbols, so lets say 94 character. So the amount of possible combination is 94^11 as Tr0ub4dor&3 as a length of 11.
Then, to get the entropy, you apply the log base 2 of the total amount of possible combination. So,
log_2(94^11) = 72 bits.
So the entropy is equal to 72. I didn’t take the time to calculate the second with the horse but it also seems to be also totally wrong..
The way*,
characters*,
combinations*
Sorry for the mistake :P
mynameisnobody wrote on 2016-04-13 at 09:59 :
“Don’t know how they get 28 bits of entropy with the first
example, this way this is calculated is for me totally wrong.”
No they are right. The base for the calculation is a randomly chose word form a ~65000 word dictionary, that gives about 16 bits of strength.
Then for every word a number of derived words are taken. For example starting with a capital or not. That results in a twofold of words to be tested, or 1 bit extra. Adding a numerical and punctuation and test all possibilities behind the base word, gives 7 bits. Not knowing the sequence of that doubles that or one extra bit. etc. etc.
Now the issue that this is a assumption that will work, is that the more permutations you apply, the less the password will be memorable. So one stops after one or 2 permutations.
My question is: What is the ideal kind of password to use for the password manager?
Let’s assume we use 20 characters. Is it more secure to:
1. Use one with completely random characters which you write down on a paper and keep it safe (or learn to remember it).
or
2. Use a certain number of uncommon words that will make up 20 characters, which you will probably be able to remember in your head.
Hi Jonathan,
choose whatever you like as long as you have at least 80 bits of security. -> “To have 80 bits of security, a password needs about 13 characters while a passphrase only needs about 5 words!”
But do NOT use your own generated passphrase with “uncommon words”. Because what is uncommon? Do you decide it? The values proposed in this post only apply to truly random chosen passphrases without any human interaction!
In my opinion, a passphrase is much better for a pasword manager because, as you already noted, is easier to remember than 13 or more characters in a randomly chosen password. ;)
OK,
What if My Name’s Fred and I create a Password [Fred_1972]
it’s 11 Characters long.
It’s Very memorable, at least to Fred,
Now suppose we scramble up the Password and change the case of some of the letters.
Now we can have multiple Passwords for multiple sites, all based on [Fred_1972]
Eg
9f1e_dR2]7[
r9F2_7][D1e
etc etc
I can have hundreds of unique passwords for different sites, all based on my 1 Master password.
Sure, if anyone works out my master password, then theoretically they can access
all my sites, but then again, if someone gets hold of the Master password to my
password manager, they get access to all my websites anyway.
Getting hold of my password strategy, eg Working out I’m using [Fred_1972]
does not give them immediate access to my sites, they must still brute force
all the variations of that and I can slow them down by using [Freddy_Oct_1972]
as my master Password.
Now the number of permutations is much higher, it’s still Trillions of Trillions
even if he works out my Master Password.
Eg my Facebook password might be [fe]yocd9_17rTsD_
Remember, an attacker doesn’t know I’m using this strategy, so as far as he is concerned, he’s still having to brute force the entire alphanumeric character set.
The advantage is, the Master password character set is highly memorable to Fred, he’s very unlikely to forget it ever, and given that, the worst case scenario is that he
could easily bruteforce it given his reduced character set being 17 characters.
An attacker however has to deal with the full alphanumeric character set.
Such a strategy might be a good compromise between having reasonable security
and the ability to be able to brute force your password should it ever be necessary.
Should an attacker know your Master Password then you are compromised, but then
you are if an attacker gets hold of your Master password to your password manager.
So what is the turning point on the number of random characters versus words?
If I am limited to a 6 character password, with just alpha numerical, no specials, or 1 or 2 random words (ie, 1 six letter word, 2 three letter words), which option is better to use?
Also what I am not sure I’m getting is, a brute force attack on 12 character password, simply tries all combinations of all characters available. If that password consists of 3 words, won’t it automatically try the words as part of its combinations it will try? In other words, if it systematically tries all combinations, the words will inevitably be part of the list of tries and it will find it.
It seems the entropy is based on the fact that the computer cracking the password is aware that words are used instead of a random string of characters. If it ignores that fact and simply brute forces it, it will find it regardless of random characters or words being used. Or what am I missing?
Thanks for the article, very interesting!
Hi dude,
many questions. ;) I’ll try to answer them:
1) If you’re limited to 6 characters than you do have a problem anyway. :) Have a look at the graph in my post: with 2 words randomly chosen out of 200k words you have 40 bits of security. This is almost the same for 6 characters randomly chosen out of alphanumerics. Hence: in theory it does not matter. (But in this bad situation I would prefer alphanumerics. For whatever reason.)
2) Yes, you’re absolutely correct: a brute-force of 12 characters will find the 3 words. But: 3 words (out of 200k) have a security level of 52 bits while 12 characters have a level of 76. That means: It would take LONGER for an attacker to brute-force your 3 words when actually brute-forcing all characters. A more realistic example: If you’re using 5 words (out of 200k) you have 88 bits while 20 characters (assuming every words has only 4 letters) have 127 bits.
3) Yes, you’re correct, even a stupid brute-force attack will find any “words”-based passphrases. Note: It always depends on the attacker. An intelligent attacker will use parallel brute-force techniques with mere character-brute-forcing and dictionary attacks etc.
Thanks so much for the time to answer, appreciate it.
I’m beginning to realize that what I am missing is an understanding of how hackers actually go about cracking passwords. I know they use databases with the most common passwords, and if they deem it worthwhile, may use social engineering to find birthdate, names of your partner, your pet, or last holiday destination, and use variations and combinations of that). What else do they do or use? And once that fails and switch to brute force, how fast can that actually go with the latest generation of 10, 12, 16 and even 32 core CPU’s? What about OpenCL and using GPU’s for password cracking?
Maybe that would be a nice blog post for you the near future ;).
Thanks again for your blog!
I have no idea who “fast they can get with current CPUs”. If you really want to crack passwords, go into the darknet or rent some cloud services with tons of tons of CPUs/GPUs and brute-force any low security password within a few seconds. ;)
I think you misunderstand. I’m not interested in cracking myself, not at all.
But a background in understanding of how it is done, and how fast a weak password can actually be cracked will help understand the need for stronger passwords with higher entropy. When I think about my own questions and some other questions here, I think there is a lot of misunderstanding in that area that leads people to believe that “123Weber321” might actually be good password for your admin account, because (and I quote):
“an attacker doesn’t know I’m using this strategy, so as far as he is concerned, he’s still having to brute force the entire alphanumeric character set.”.
And that is simply not true.
Hence, my comment to gain an understand of how it’s actually done will help understanding the need for better, more secure passwords.
“So: don’t ever use only digits for critical passwords!”
Wrong! If you don’t tell the hacker then he could have no way of knowing that you had only used digits, so would have to brute force the entire character set. Perfectly fine to only use digits as long as you don’t tell anyone.
This advice is only correct to system providers who explicitly tell their users that their password routine only accepts digits. THEN you have a weakened password system.
Hi Alan,
in fact, if the attacker does not know the “entropy” which he must brute-force, you might have a small advantage.
However, you’re assuming a stupid attacker who brute-forces the entires character set sequentially. A more profound attacker will use high parallel optimization and some kind of “best practices” for brute-forcing passwords. Hence: he will definitely first try some small characters sets (such as only digits or only small letters) before he will try some huge character sets.
A question : Suppose i use a pw such as @AbCd1234567890@ which is 16 chars how insecure is this?
Horribly insecure, cause it is not generated randomly but highly guessable.
(Have you read the article? ;D “I assume that each character (or word) of the password is chosen completely random!”)
keyspace= 104 length= 16
E= 107.20703549025747
Thank you for illuminating me!
I’ve been reading up on the subject and on the use of passphrases I have a question: would a multi-lingual passphrase add to its strength in some way?
Construct the passphrase from randomly generated words using different language dictionaries? Or translate a few words (after generating a passphrase in your native language) into more than one language that you feel comfortable with?
Hey Peter,
yes, this would increase the overall entropy, but not that much. Have a look at my first figure and compare the two lines for “200k words” and “500k words”. The differences are not that much.
To have a more secure passphrase, simply increase your passphrase from 4 words to 6 (or even to 8). This has a much more dramatic effect on the entropy!
This may have been covered and I just didn’t understand it, but if I use a passphrase but replace some of the letters with numbers/symbols, does that actually increase the entropy at all?
For example:
NeverEatSoggyWaffles (not a good phrase as it is common, just using it as an example)
vs
N3verE@tS0ggyWaffles
To the point of the xkcd comic, remembering which letters were replaced with what makes it harder to remember or type in, but if it adds enough complexity to increase the entropy a worthwhile amount, then it may be worth it. Especially for something like a master password for a password manager
Also, I know this is an old post, but still very relevant, so I’m thankful you did it!
Hey Kelly,
it’s only called entropy when you’re choosing something merely by random. You’re trying to do some substitution. This might add some complexity, but not entropy. (Just taking about the wording right here.)
Anyway, if you want to use a passphrase out of words, which is chosen by random, then you can increase your security by randomly generating a passphrase with a few more words. ;)
If you have chosen your passphrase by yourself it will have a horribly entropy at all! While you might improve the security level a bit by doing a substitution of some characters, this might not pay out. Especially not for a master passphrase. (Though I haven’t done the math right now. Of course, it depends on how many characters out of your passphrase you’re substituting. If you substitute *every* character (ridiculous), it will be hard. Haha. If you only substitute one single char, it won’t be really more secure than.)
If your’re using a substitution, you should use a random substitution method. (Again, it’s about the randomness.) Using something like the well-known “a -> @” and the like won’t be a good decision at all. The password-cracking tools out there know those common substitution methods.
Finally, I’m not sure whether its easier for a human to remember several substitutions compared to a random generated passphrase.
To be little more positive at the end: If you want to generate something by yourself, write down a whole sentence with at least 12-16 words. Use the very first character of those words as your starting point. Now add some special characters and numbers to this. Not only at the end, but in the middle somewhere. You can also use your substitution idea as well, even with the basic “a -> @ stuff”. In the end, you have a password which is about 20 characters long, will be easy to remember to you, and will have a good security level. (Though NOT chosen randomly.) But a password-cracking can only “solve” it by brute-force – which won’t be fast at all.
Thanks for the question. I enjoyed to think about it once again.
Johannes